Home
Scientific
Program Registration
Excursion Travel
Accommodation
Slides Schedule & Book of Abstracts Sponsors Participants Simulations
Slides Schedule & Book of Abstracts Sponsors Participants Simulations
Some PINT simulations

Parallel-in-time solution snapshots (using XBraid) of the velocity magnitude at the 5120th time step (t=2.56s), for unsteady vortex shedding and the compressible Navier-Stokes equations
(Courtesy of J. B. Schroder)

Simulation of the plasma in the ITER tokamak, using parareal
(Courtesy of D. Samaddar)

Approximate
solution
obtained by the time parallel algorithm using diagonalization
(Courtesy of L. Halpern)
(Courtesy of L. Halpern)
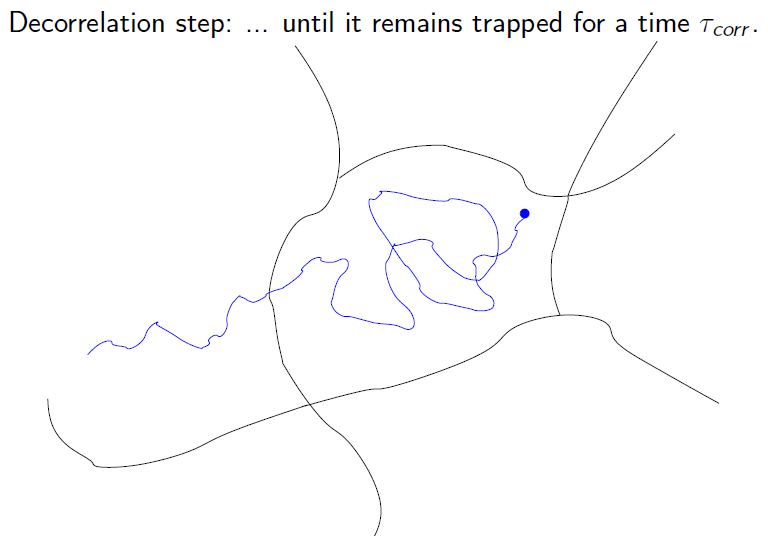
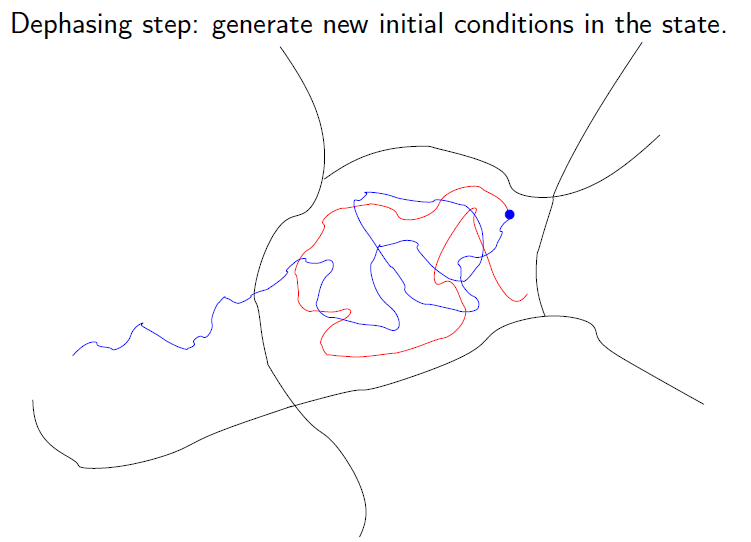
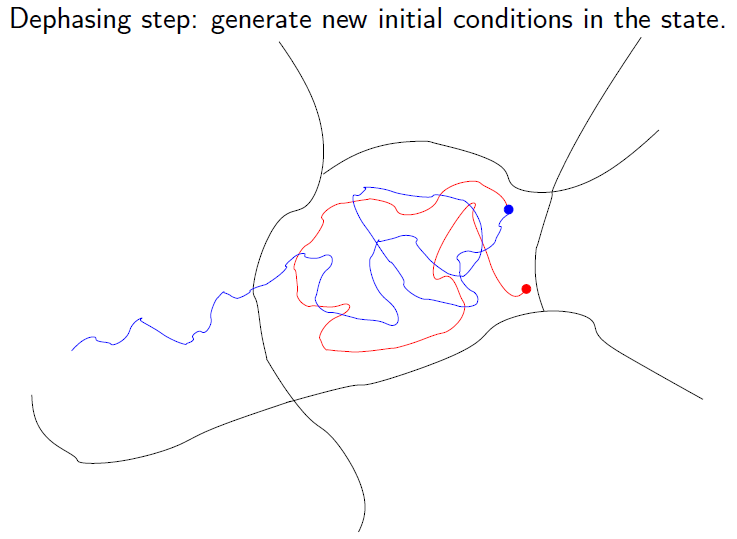
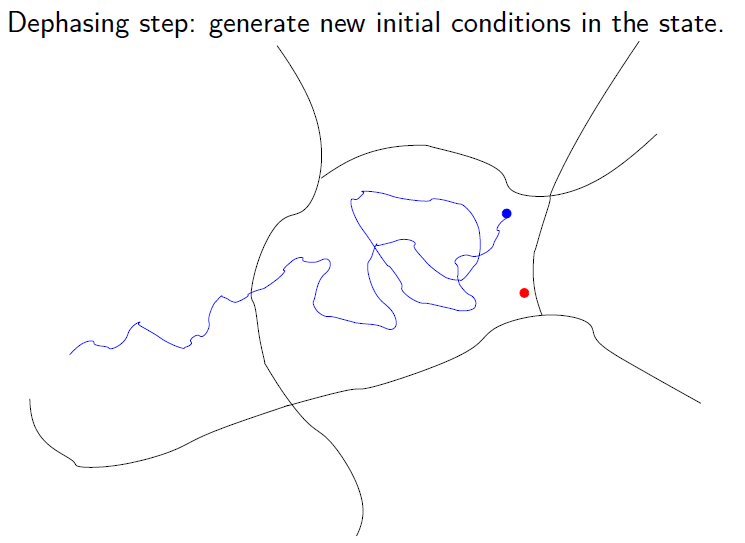
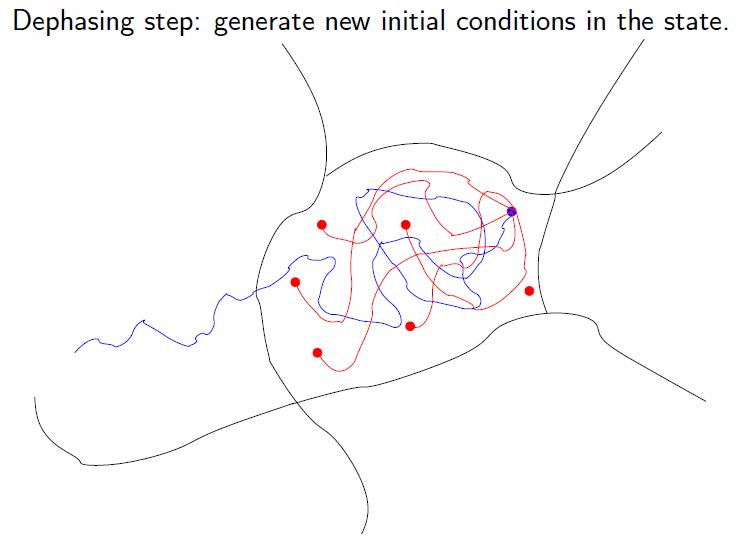
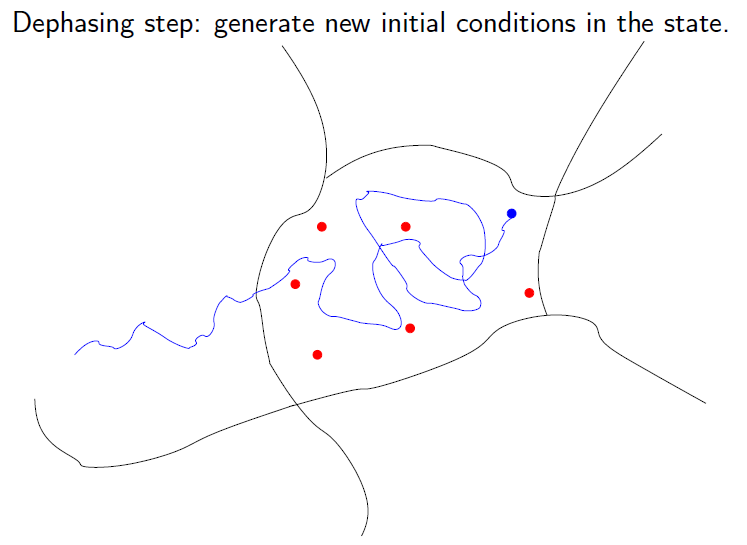
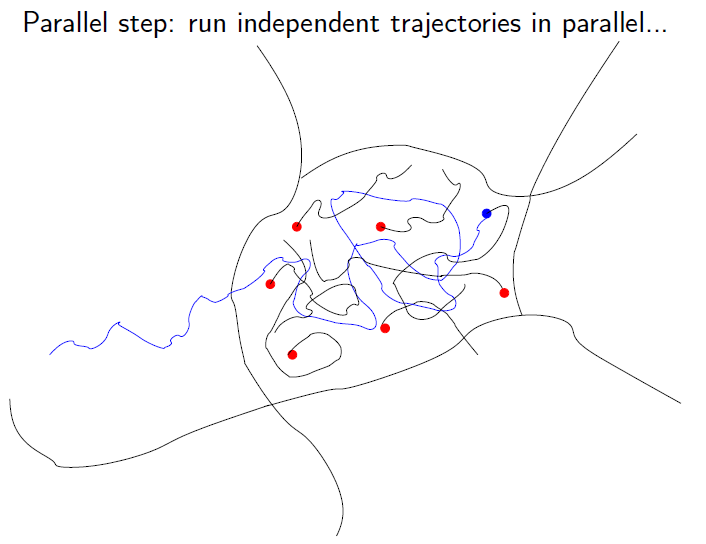
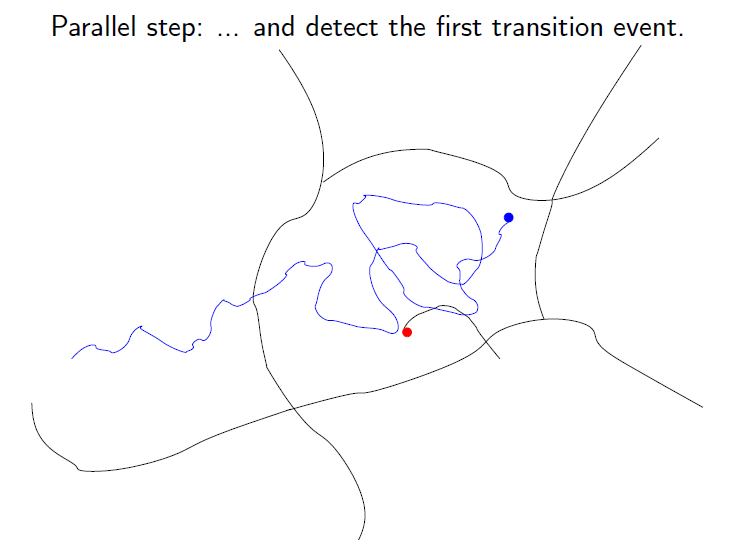
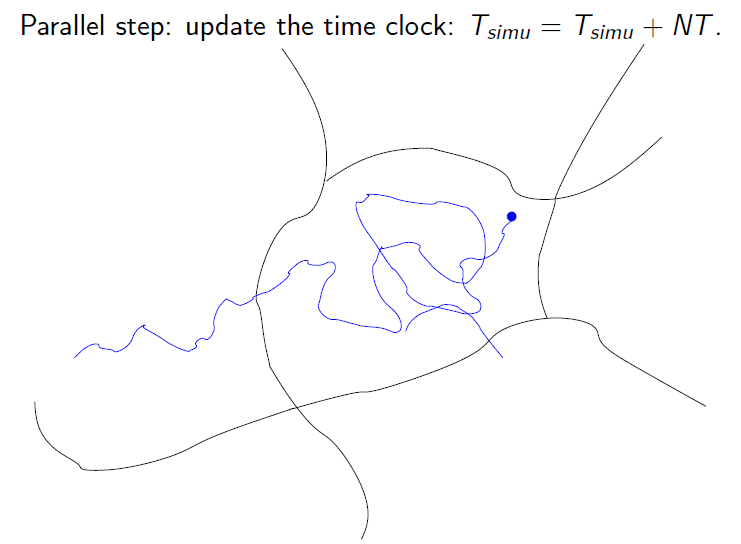
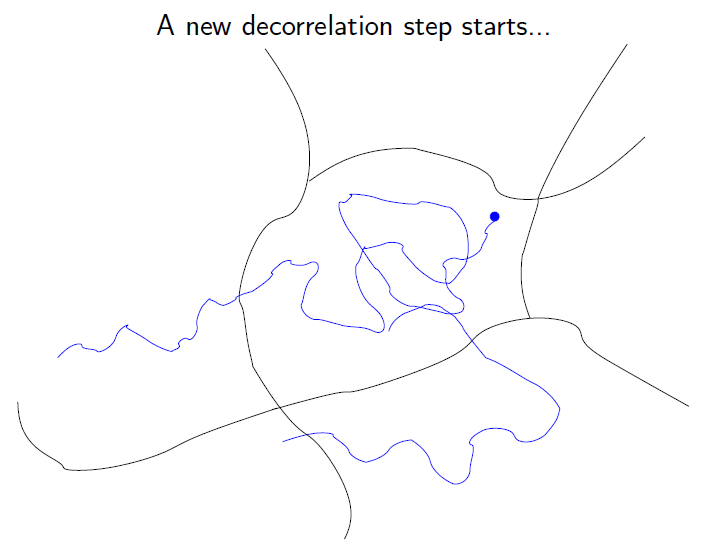
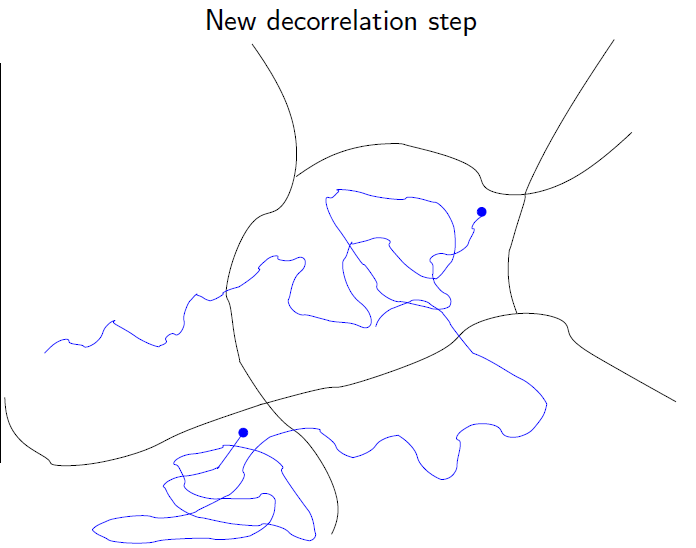
Parallel Replica
Algorithm for molecular dynamics. Parallel step:
run independent trajectories in parallel (left), and detect the first transition event (right)
(Courtesy of T. Lelièvre)
run independent trajectories in parallel (left), and detect the first transition event (right)
(Courtesy of T. Lelièvre)


Symplectic
parareal schemes and structure preserving parallel in time
propagators.
The right figure shows the energy conservation, after 3 iterations
of the algorithm,
for a solar system problem
(Courtesy of G. Turinici)
(Courtesy of G. Turinici)

Coupled
Parareal - Optimized Schwarz Waveform Relaxation method, where few
(P) iterations of OSWR in the fine propagator are done, for
solving advection-reaction-diffusion problems
(Courtesy of B. D. Quang)
(Courtesy of B. D. Quang)
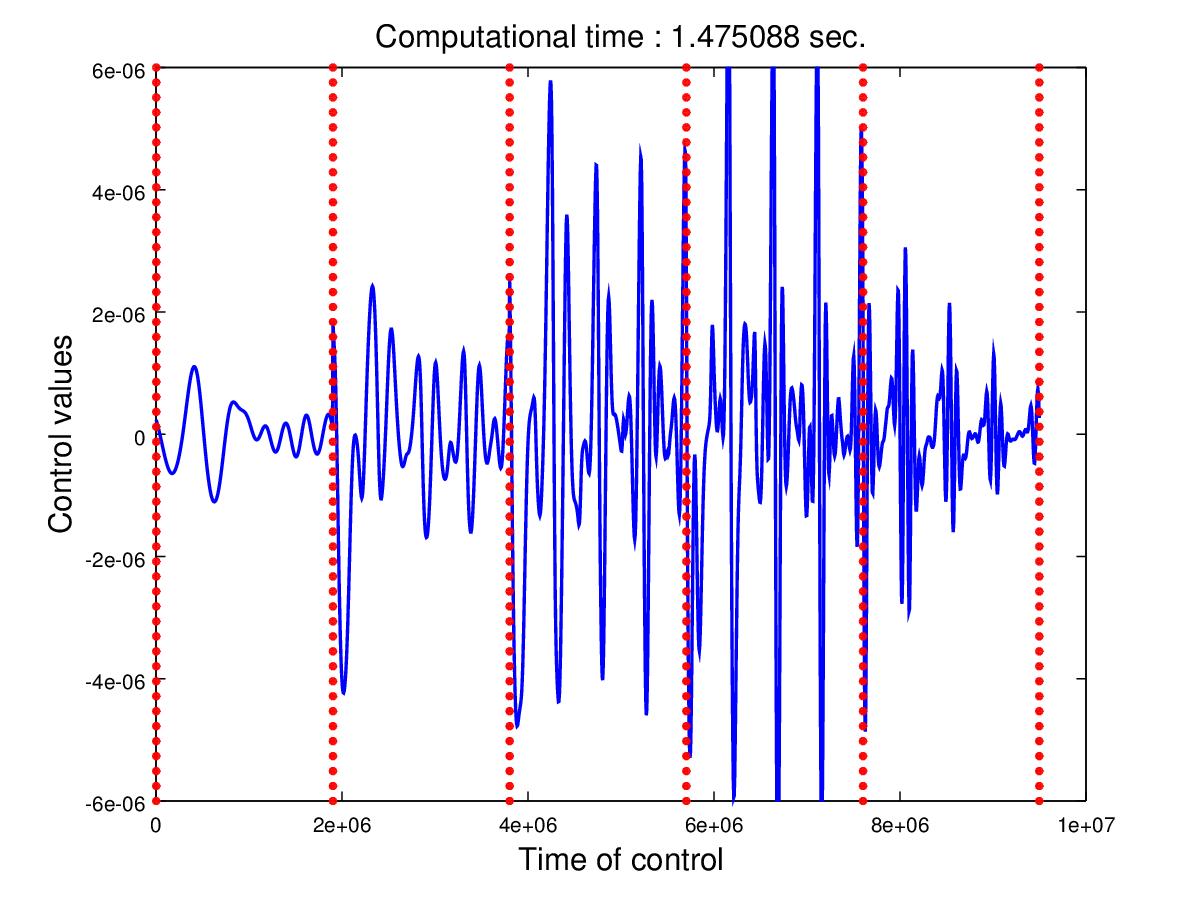
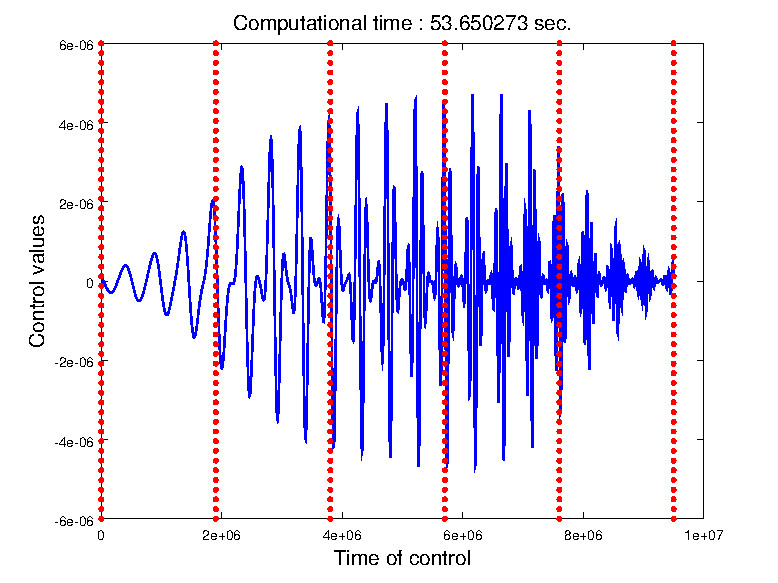
Parareal
algorithm for optimal control
(Courtesy of J. Salomon)
(Courtesy of J. Salomon)


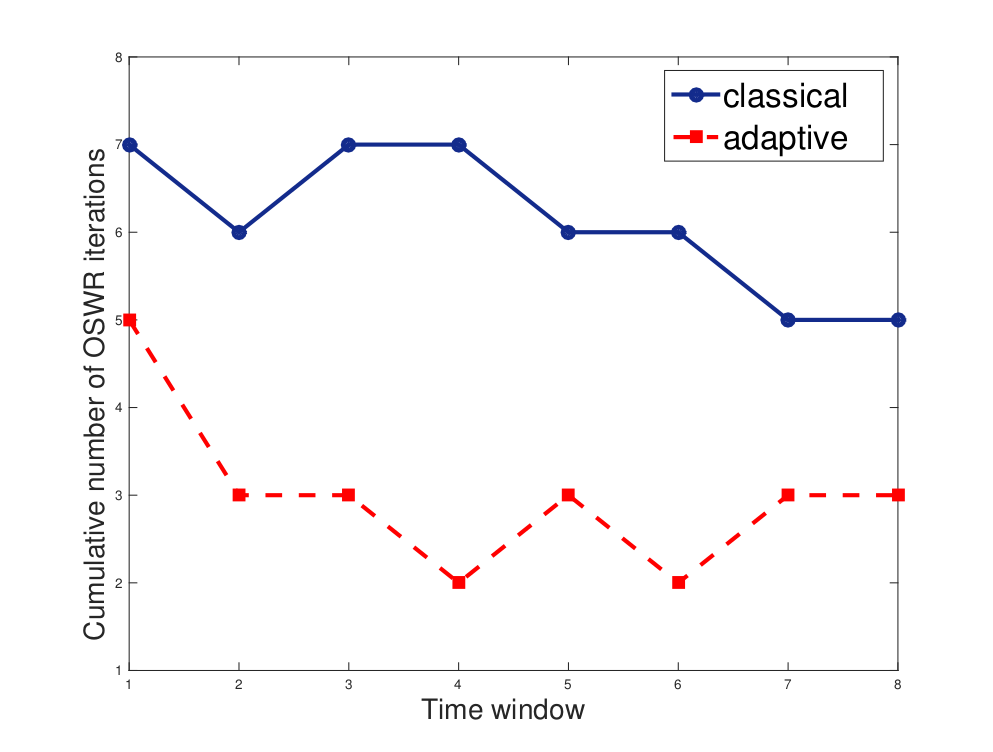
A
posteriori stopping criteria for global-in-time domain decomposition
for the heat equation in mixed formulations (Andra test case)
(Courtesy of S. Ali Hassan)
for the heat equation in mixed formulations (Andra test case)
(Courtesy of S. Ali Hassan)

A
posteriori stopping criteria for global-in-time domain decomposition
for two-phase flow between different rock types
(Dense Non-Aqueuous Phase Liquid (DNAPL) infiltration in a
low-capillarity lens
(Courtesy of E. Ahmed)
(Courtesy of E. Ahmed)


Others
applications of parallel-in-time methods are :
weather forecast, thermal-hydraulic modeling of a real life accidental transient of a reactor, with stiff terms and bifurcations (CATHARE, see the ANR project CINE-PARA), ...
see also www.parallelintime.org
weather forecast, thermal-hydraulic modeling of a real life accidental transient of a reactor, with stiff terms and bifurcations (CATHARE, see the ANR project CINE-PARA), ...
see also www.parallelintime.org